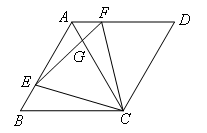
已知菱形ABCD,E,F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论:
①△ABC与△ADC均为等边三角形;②△BEC≌△AFC;③△ECF为等边三角形;④若AF=1,则EF= .其中正确的有几个( )
.其中正确的有几个( )
- A.1
- B.2
- C.3
- D.4
答案
正确答案:D
知识点:略
①由菱形性质可得,AB=BC=CD=DA,∠B=∠D=60°
故△ABC与△ADC均为等边三角形,正确;
②由①可得,CA=BC,∠B=∠CAD=60°,且BE=AF
∴△BEC≌△AFC(SAS),故正确;
③由②,∠BCE=∠AFC,EC=FC
∴∠FCE=∠ACF+∠ACE=∠BCE+∠ACE=∠ACB=60°
∴△ECF为等边三角形,正确;
④如图,过点F作FH⊥EA,交EA延长线于点H
△AEF中,∠EAF=120°,AF=1,AE=AB-BE=3
则Rt△FAH中可得,![]() ,
,![]()
∴Rt△FEH中,由勾股定理可得![]() ,故正确.
,故正确.
综上,正确的为①②③④.
略








