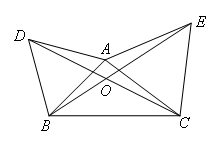
如图，△ABD与△AEC都是等边三角形，AB≠AC，有以下结论：①BE=CD；②∠BOD=60°；③∠BDO=∠CEO；④若∠BAC=90°，且DA∥BC，则BC⊥CE，其中正确的结论有(    )

如图，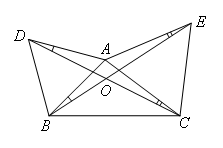

①BE=CD
∵△ABD与△AEC都是等边三角形，
∴AB=AD，AC=AE，∠DAB=∠CAE=60°，
∴∠DAB+∠BAC=∠CAE+∠BAC，
即∠DAC=∠BAE，
∴△ADC≌△ABE（SAS），
∴BE=CD．
②∠BOD=60°
∵△ADC≌△ABE，
∴∠ADC=∠ABE．
∵∠DOE是△OBD的一个外角，
∴∠DOE=∠ODB+∠OBD=∠ODB+∠DBA+∠ABE=∠ODB+∠DBA+∠ADC=∠ADB+∠DBA=120°
∴∠BOD=60°．
③∠BDO=∠CEO
∵△ADC≌△ABE，
∴∠ADC=∠ABE，
∵AB≠AC，
∴AB≠AE，
∴∠ABE≠∠AEB，
∴∠ADC≠∠AEB，
由题意得∠BDO=∠ADB-∠ADC，∠CEO=∠AEC-∠AEB，
∵∠ADB=∠AEC=60°，∠ADC≠∠AEB，
∴∠BDO≠∠CEO．
④若∠BAC=90°，且DA∥BC，则BC⊥CE
∵∠DAB=∠ACE=60°，∠BAC=90°，
∴∠DAC=∠DAB+∠BAC=150°，
∵DA∥BC，
∴∠BCA=30°，
∴∠BCE=∠BCA+∠ACE=90°，
∴BC⊥CE．
综上所述，①②④正确．

略