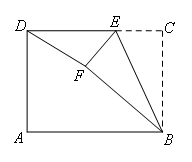
如图,长方形ABCD中,AB=4,BC=3,点E是CD边上一点,连接BE,把∠C沿BE折叠,使点C落在点F处.当△DEF为直角三角形时,DE的长为( )
- A.1
- B.1或
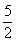
- C.
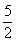
- D.3或
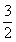
答案
正确答案:B
知识点:略
∵四边形ABCD是长方形,
∴AB=CD=4,AD=BC=3,
分两种情况讨论:
①当∠FED=90°时,如图所示,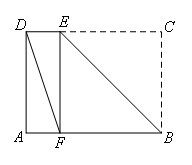
则∠CEF=90°,
由折叠的性质得:CE=FE=BC=3,
∴DE=CD-CE=1;
②当∠DFE=90°时,如图所示,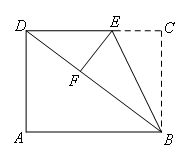
在Rt△ABD中,∠A=90°,AB=4,AD=3,
∴BD=5,
由折叠的性质得:∠BFE=∠C=90°,BF=BC=3,EF=EC,
∴∠DFE=∠BFE=90°,即点B,F,D三点共线,点F在BD上,
∴DF=BD-BF=5-3=2,
设DE=x,则EF=CE=4-x
在Rt△DEF中,∠EFD=90°,DE=x,EF=4-x,DF=2,
由勾股定理得,![]()
解得,![]()
综上所述,DE的长为1或![]() ;
;
故选B.
略








