如图,在△ABC中,∠B=67°,∠C=33°,AD平分∠BAC,则∠ADC的度数为( )
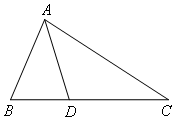
- A.80°
- B.107°
- C.73°
- D.100°
答案
正确答案:B
如图,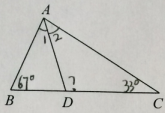
结合已知条件,∠ADC可以看作△ACD的内角,也可以看作
△ABD的一个外角,因此有两种思路.
第一种思路:
将∠ADC看作△ACD的内角:
在△ABC中,∠B=67°,∠C=33°,
根据三角形的内角和等于180°,得∠BAC=80°;
由AD平分∠BAC,根据角平分线的定义,得![]() .
.
在△ACD中,∠2=40°,∠C=33°,
根据三角形的内角和等于180°,得∠ADC=107°.
第二种思路:
将∠ADC看作△ABD的一个外角:
已知在△ABC中,∠B=67°,∠C=33°,
根据三角形的内角和等于180°,得∠BAC=80°;
由AD平分∠BAC,根据角平分线的定义,得![]() .
.
∠ADC是△ABD的一个外角,根据三角形的外角等于与它不相
邻的两个内角的和,得∠ADC=∠B+∠1=67°+40°=107°.
故选B.
略








