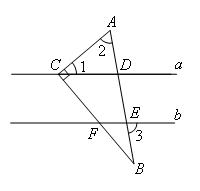
已知：如图，将Rt△ABC的直角顶点C放在直线a上，∠1=50°，∠2=60°，∠3=70°．
求证：a∥b．


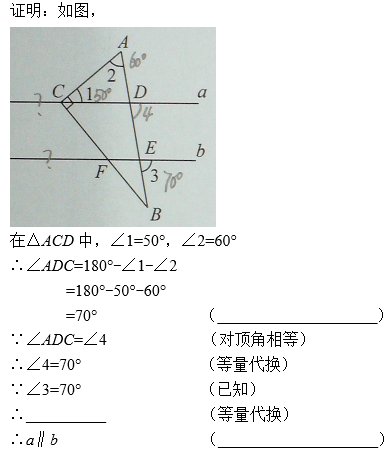
①三角形的内角和等于180°；②平角的定义；③∠3=∠4；④∠3=∠D；
⑤同位角相等，两直线平行；⑥两直线平行，同位角相等．
以上空缺处依次所填正确的是(    )

在△ACD中，已知∠1与∠2，
利用三角形内角和等于180°，可以求出∠ADC的度数；
进而利用对顶角相等，求得∠4的度数；
最后利用同位角相等，两直线平行证明a∥b．
第一个空：在△ACD中，已知∠1=50°，∠2=60°，
求得∠ADC=180°-∠1-∠2=180°-50°-60°=70°；
所以依据是三角形的内角和等于180°，故①正确．
第二个空：条件是∠4=70°，∠3=70°，依据是等量代换，
所以第二个空中的结论为∠3=∠4，③正确；
第三个空：∠3和∠4是直线a和直线b被直线AB截得的同位角，由同位角相等，得两直线平行，因此依据是同位角相等，两直线平行，⑤正确．
综上所述，依次所填正确的是①③⑤，故选A．

略