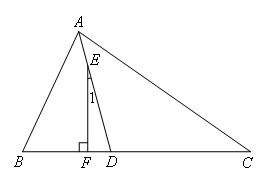
已知：如图，在△ABC中，AD平分∠BAC，E为AD上一点，且EF⊥BC于点F．
若∠C=35°，∠1=15°，求∠B的度数．

解：如图，

∵∠EDF是△ADC的一个外角（外角的定义）
∴∠EDF=∠DAC+∠C（三角形的一个外角等于和它不相邻的两个内角的和）
∵∠C=35°（已知）
∴∠DAC=∠EDF-∠C
=75°-35°
=40°（等式的性质）
∵AD平分∠BAC（已知）
∴∠BAC=2∠DAC
=2×40°
=80°（角平分线的定义）
∴∠B=180°-∠BAC-∠C
=180°-80°-35°
=65°（三角形的内角和等于180°）
横线处应填写的过程最恰当的是( )

A.∵∠EFD=90°（已知）
∴∠1+∠EDF=90°（直角三角形两锐角互余）
∵∠1=15°（已知）
∴∠EDF=90°-∠1=90°-15°=75°（等式的性质）
B.∵EF⊥BC（已知）
∴∠EFD=90°（垂直的定义）
∴∠EDF=90°-∠1=90°-15°=75°（直角三角形两锐角互余）
C.∵EF⊥BC（已知）
∴∠EFD=90°（垂直的定义）
∴∠1+∠EDF=90°（直角三角形两锐角互余）
∵∠1=15°（已知）
∴∠EDF=90°-∠1=90°-15°=75°（等式的性质）
D.∵EF⊥BC（已知）
∴∠EFD=90°（垂直的定义）
∵∠ADC是△ABD的一个外角（外角的定义）∴∠ADC=∠1+∠EFD（三角形的一个外角等于和它不相邻的两个内角的和）
∵∠1=15°（已知）
∴∠ADC=15°+90°=105°（等量代换）

答案

正确答案：C

略

下载次数：0