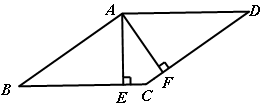
如图,在平行四边形ABCD中,AE⊥BC于E,AF ⊥CD于F,∠EAF=45°,且AE+AF=2 ,则平行四边形ABCD的周长是______.
答案
因为四边形ABCD为平行四边形,AE⊥BC,AF⊥CD,所以∠EAD=∠AFD=90°,又因为∠EAF=45°,所以∠FAD=45°,∠ADF=45°,则∠ABE=45°,因此AE=BE,AF=FD,根据勾股定理可知,AB=AE,AD=
AF,而四边形ABCD的周长为C=2(AB+AD)=2
(AE+AF),又因为AE+AF=2
,所以平行四边形ABCD的周长C=2
×2=4
.
不能很好的利用平行四边形的性质及特殊直角三角形的性质.








