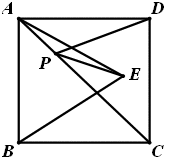
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
- A.
- B.
- C.3
- D.
答案
正确答案:A
知识点:两点间的距离
如图,连接PB.因为四边形ABCD为正方形,AC为对角线,所以AB=AD,∠BAP=∠DAP,则易证△BAP≌△DAP,所以PB=PD,因此PD+PE=PB+PE.在△PBE中,PB+PE≥BE,又因为△ABE为等边三角形,所以BE=AB,因正方形的面积为12,所以BE=AB=,故PB+PE≥
,即PD+PE≥
.当点P与B、E均共线时,能取最小值.故答案为:A
不能找到合适的辅助线








